Por Rafael González Acuña
¿Te ha pasado que, cuando miras a través de una cámara fotográfica, un telescopio, unos binoculares o un microscopio, ves las imágenes borrosas o sin nitidez? Probablemente no es que el lente esté sucio o fuera de foco, sino que se trata de un fenómeno óptico llamado aberración esférica.
La aberración es un defecto de los sistemas ópticos, que hacen que la imagen formada por una lente sea borrosa o distorsionada, y la naturaleza de dicha distorsión depende del tipo de aberración.
Un sistema óptico de formación de imágenes que presente aberración producirá una imagen sin nitidez. Es ahí cuando los fabricantes de instrumentos ópticos deben corregir los dispositivos para compensar la aberración.
La aberración esférica es un tipo de aberración óptica que se encuentra en los sistemas ópticos que utilizan superficies esféricas, como cámaras fotográficas, telescopios, binoculares, microscopios, etcétera. Las lentes y los espejos curvos de estos equipos se hacen generalmente con superficies que son esféricas, porque esta forma es más fácil de formar que las superficies curvadas no esféricas. Los rayos de luz que inciden en una superficie esférica descentrados se refractan o se reflejan más o menos que los que impactan cerca del centro. Esta desviación reduce la calidad de las imágenes producidas por los equipos ópticos.
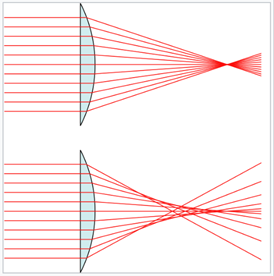
La solución al problema de la aberración esférica (establecido por Wasserman-Wolf en 1949)
Una lente asférica es una lente cuyas superficies no son porción de una esfera, sino que tienen una forma más libre, por ejemplo, el lente de una cámara fotográfica.
Una lente asférica puede reducir o eliminar la aberración esférica y también reducir otras aberraciones ópticas como el astigmatismo, en comparación con una lente esférica simple. Una sola lente asférica a menudo puede reemplazar un sistema de lentes múltiples mucho más complejo. El dispositivo resultante es más pequeño y liviano, y algunas veces más barato que el diseño de lentes múltiples.
En el diseño de sistemas ópticos, la superficie asférica tiene como objetivo reducir fuertemente la aberración esférica. Muchos autores propusieron un diseño de lentes con dos superficies asféricas para corregir la aberración esférica, pero en sí todas las soluciones son de carácter numérico.
El problema del diseño de un lente sin aberración esférica también se conoce como el problema de Wasserman-Wolf, postulado por Wasserman y Wolf en 1949 en un artículo publicado en la Royal Society Proceedings, el cual explica de forma técnica el problema, pero no da una solución analítica.
Sin embargo, el problema de Wasserman-Wolf es más antiguo, y en efecto debe ser tan antiguo como las mismas lentes, pues en un libro muy antiguo de 1690, titulado «Tratado sobre la luz», del astrónomo Christian Huygens, menciona que el problema ya era popular en la época y que Newton y Leibniz estaban interesados en resolverlo, pero no pudieron.
En un libro del siglo XVII se menciona que los astrónomos Newton y Leibniz estaban detrás del mismo problema óptico.
En un libro del siglo XVII se menciona que los astrónomos Newton y Leibniz estaban detrás del mismo problema óptico.En un artículo científico llamado “General formula for bi-aspheric singlet lensdesign free of spherical aberration”, que publicamos recientemente en la revista Applied optics, ofrecemos la ecuación que da solución a la conjetura de Wasserman-Wolf, la cual se muestra en la figura 2.
En dicha ecuación describimos cómo debe ser la forma de la segunda superficie asférica de la lente dada una primera superficie, la cual es proporcionada por el usuario, así como la distancia objeto-imagen. La segunda superficie es tal que corrige toda la aberración generada por la primera superficie, y se elimina la aberración esférica.
Durante nuestro estudio calculamos la eficiencia de 500 rayos, y el promedio de satisfacción de todos los ejemplos fue de 99.9999999999%. Este hallazgo podrá tener muchas aplicaciones, ya que permitirá producir lentes con mayor calidad de imagen a cualquier distancia, cualquier grosor y cualquier material.
Con este resultado se concluyen siete décadas de búsqueda por la solución del problema de Wasserman-Wolf.
La solución del problema de Levi-Civita (establecido en 1900)
Por otra parte, el problema general de los óvalos cartesianos fue considerado por primera vez por el físico matemático italiano Levi-Civita en 1900, sin dar una fórmula analítica de forma cerrada. El problema del óvalo cartesiano generalizado consiste en encontrar una superficie refractiva que transforme un frente de onda entrante, en otro frente de onda saliente esférico.
En una publicación presentada junto con los investigadores Alejandro Chaparro Romo y Julio Gutiérrez Vega en la revista Applied Optics, bajo el título “General formula to design freeform singlet free of spherical aberration and astigmatism”, damos una respuesta analítica a este antiguo problema.
Con dicha publicación se obtiene la respuesta a un problema que tenía más de un siglo sin solución, y la cual se consideraba un mito por la comunidad científica especializada.
En resumen, ambas soluciones presentadas por nuestro equipo de investigadores tienen un enorme potencial en el diseño de dispositivos ópticos, y sus aplicaciones son muchísimas, particularmente en el diseño de lentes, cámaras, microscopios, telescopios, endoscopios, etcétera, los cuales se caracterizan por tener una altísima calidad de imagen.
Otro aspecto a resaltar es que no solo encontramos las soluciones de ambas conjeturas, sino que dichas soluciones son únicas, por lo que ambas ecuaciones perdurarán a través del tiempo.
——————————
Rafael Guillermo González Acuña estudió Ingeniería Física Industrial en el Tecnológico de Monterrey y cursó la Maestría en Optomecatrónica en el Centro de Investigaciones en Óptica, A.C. Actualmente estudia el Doctorado en Nanotecnología en el Tecnológico de Monterrey. Su tesis doctoral se enfoca en el diseño de lentes libres de aberración esférica.
